BudgetIV: partial identification of causal effects with mostly invalid isntruments

Introduction

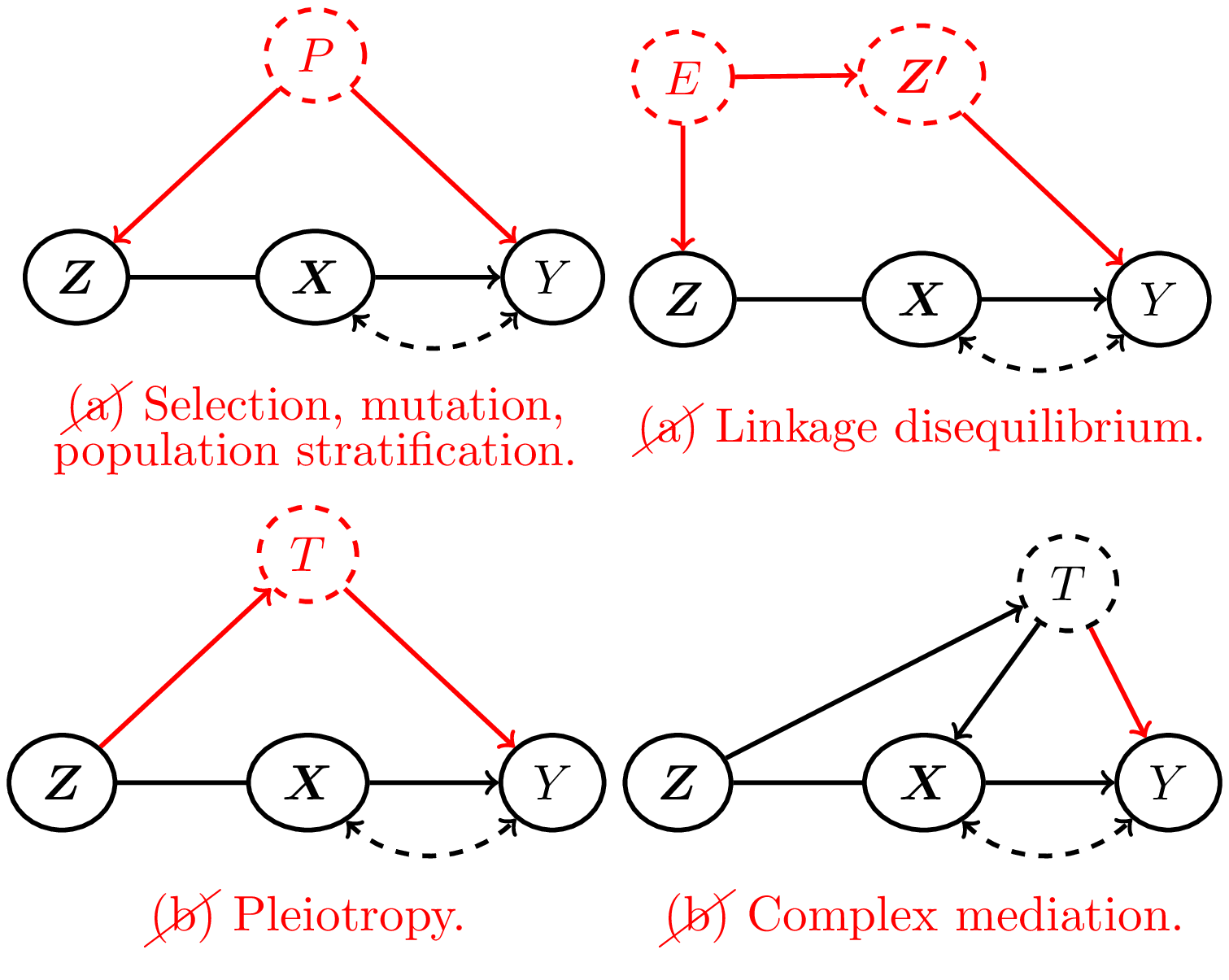
budgetIV provides a tuneable and interpretable method for relaxing the instrumental variables (IV) assumptions to infer treatment effects in the presence of unobserved confounding. For a pre-treatment covariate to be a valid IV, it must be (a) unconfounded with the outcome and (b) have a causal effect on the outcome that is exclusively mediated by the exposure. It is impossible to test the validity of these IV assumptions for any particular pre-treatment covariate; however, when different pre-treatment covariates give differing causal effect estimates if treated as IVs, then we know at least one of the covariates violates these assumptions. budgetIV exploits this fact by taking as input a minimum ‘’budget’’ of pre-treatment covariates assumed to be valid IVs. This can be extended to assuming a set of budgets for varying ‘’degrees’’ of validity set by the user and defined formally through a parameter that captures violation of either IV assumption. These budget constraints can be chosen using specialist knowledge or varied in a principled sensitivity analysis. budgetIV supports non-linear treatment effects and multi-dimensional treatments; requires only summary statistics rather than raw data; and can be used to construct confidence sets under a standard assumption from the Mendelian randomisation literature. With one-dimensional \(\Phi (X)\), a computationally-efficient variant Budget_IV_Scalar allows for use with thousands of pre-treatment covariates.

We assume a heterogenous treatment effect, implying the following structural causal model: \[Z := f_z (\epsilon_z),\] \[X := f_x (Z, \epsilon_x),\] \[Y = \theta \Phi (X) + g_y (Z, \epsilon_y).\] There may be association between \(\epsilon_y\) and \(\epsilon_z\), indicating a violation of the unconfoundedness assumption (a); and \(g_y\) may depend on \(Z\), indicating violation of exclusivity (b). With budgetIV, the user defines degrees of validity \(0 \leq \tau_1 \leq \tau_2 \leq \ldots \leq \tau_K\) that may apply to any candidate instrument \(Z_i\). If \(Z_i\) satisfies the \(j\)’th degree of validity, this means \(\lvert \mathrm{Cov} (g_y (Z, \epsilon_y), Z_i) \rvert \leq \tau_j\). Choosing \(\tau_1 = 0\) would demand some pre-treatment covariates give valid causal effect estimates, while choosing \(\tau_K = \infty\) would allow for some covariates to give arbitrarily biased causal effect estimates if treated as IVs. budgetIV will return the corresponding identified/confidence set over causal effects that agree with the budget constraints and with the user-input summary statistics: beta_y corresponding to \(\mathrm{Cov} (Y, Z)\) and beta_Phi corresponding to \(\mathrm{Cov} (\Phi (X), Z)\). Other regression coefficients such as odds ratios, hazard ratios or multicolinearity-adjusted regression coefficients may be used for beta_y and beta_Phi, but this also changes the interpretation of the \(\tau\)’s.

For further methodological details and theoretical results and advanced use cases, please refer to Penn et al. (2024) doi:10.48550/arXiv.2411.06913.

Installation

To install the development version from GitHub, using devtools, run:

devtools::install_github('jpenn2023/budgetivr')

library(budgetivr)

Examples

First, we calculate summary statistics from the example dataset:

data(simulated_data_budgetIV)

beta_y <- simulated_data_budgetIV$beta_y

beta_phi_1 <- simulated_data_budgetIV$beta_phi_1
beta_phi_2 <- simulated_data_budgetIV$beta_phi_2

beta_phi <- matrix(c(beta_phi_1, beta_phi_2), nrow = 2, byrow = TRUE)

delta_beta_y <- simulated_data_budgetIV$delta_beta_y

Then, we define the basis functions \[\Phi (X)\] and set background budget constraints:

phi_basis <- expression(x, x^2)

tau_vec = c(0)
b_vec = c(3)

Then, we define the baseline treatment \[x_0\] and the treatment values to calculate the average treatment effect over:

X_baseline <- list("x" = c(0))

x_vals <- seq(from = 0, to = 1, length.out = 500)

ATE_search_domain <- expand.grid("x" = x_vals)

Now we run budgetIV to partially identify the budget assignments and corresponding average causal effect bounds:

partial_identification_ATE <- budgetIV(beta_y = beta_y,
                                       beta_phi = beta_phi,
                                       phi_basis = phi_basis,
                                       tau_vec = tau_vec,
                                       b_vec = b_vec,
                                       ATE_search_domain = ATE_search_domain,
                                       X_baseline = X_baseline,
                                       delta_beta_y = delta_beta_y)