jti: Junction Tree Inference

R buildstatus

About

The jti package (pronounced ‘yeti’) is a memory efficient implementaion of the junction tree algorithm (JTA) using the Lauritzen-Spiegelhalter scheme. Why is it memory efficient? Because we use a sparse representation for the potentials which enable us to handle large and complex graphs where the variables can have an arbitrary large number of levels. The jti package is a big part of the software paper sparta: Sparse Tables and their Algebra with a View Towards High Dimensional Graphical Models.

Installation

Current stable release from CRAN:

install.packages("jti")

Development version (see README.md for new features):

devtools::install_github("mlindsk/jti", build_vignettes = FALSE)

Libraries

library(jti)
library(igraph)

Setting up the network

el <- matrix(c(
  "A", "T",
  "T", "E",
  "S", "L",
  "S", "B",
  "L", "E",
  "E", "X",
  "E", "D",
  "B", "D"),
  nc = 2,
  byrow = TRUE
)

g <- igraph::graph_from_edgelist(el)
plot(g)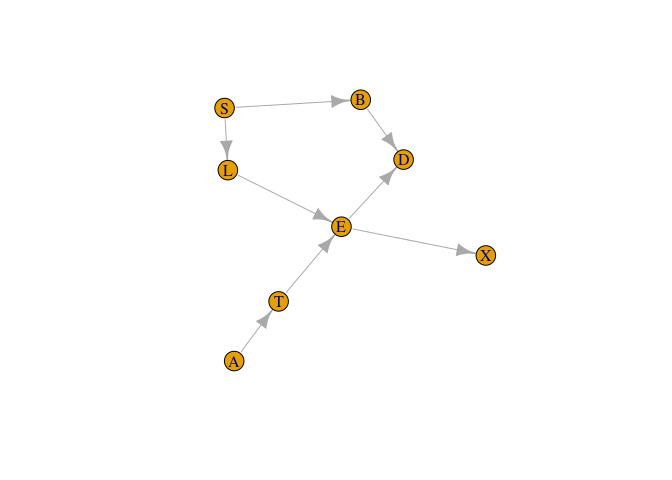

We use the asia data; see the man page (?asia)

Compilation

Checking and conversion

cl <- cpt_list(asia, g)
cl
#>  List of CPTs 
#>  -------------------------
#>   P( A )
#>   P( T | A )
#>   P( E | T, L )
#>   P( S )
#>   P( L | S )
#>   P( B | S )
#>   P( X | E )
#>   P( D | E, B )
#> 
#>   <bn_, cpt_list, list> 
#>  -------------------------

Compilation

cp <- compile(cl)
cp
#>  Compiled network  (cpts initialized) 
#>  ------------------------------------ 
#>   Nodes: 8 
#>   Cliques: 6 
#>    - max: 3 
#>    - min: 2 
#>    - avg: 2.67
#>   <bn_, charge, list> 
#>  ------------------------------------
# plot(get_graph(cp)) # Should give the same as plot(g)

After the network has been compiled, the graph has been triangulated and moralized. Furthermore, all conditional probability tables (CPTs) has been designated to one of the cliques (in the triangulated and moralized graph).

Example 1: sum-flow without evidence

jt1 <- jt(cp)
jt1
#>  Junction Tree 
#>  ------------------------- 
#>   Propagated: full 
#>   Flow: sum 
#>   Cliques: 6 
#>    - max: 3 
#>    - min: 2 
#>    - avg: 2.67
#>   <jt, list> 
#>  -------------------------
plot(jt1)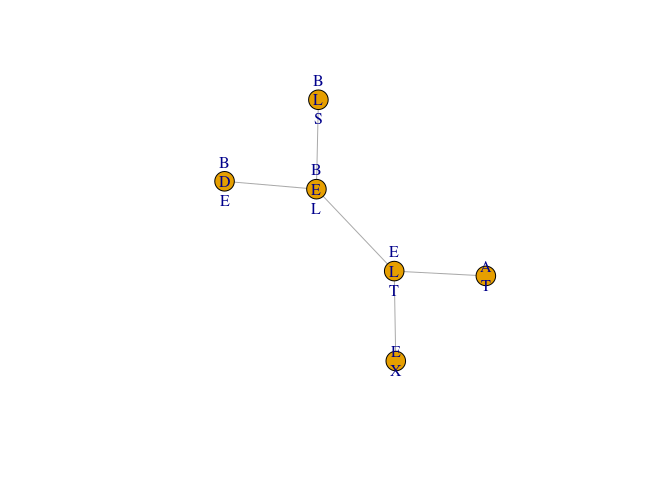

Query probabilities

query_belief(jt1, c("E", "L", "T"))
#> $E
#> E
#>         n         y 
#> 0.9257808 0.0742192 
#> 
#> $L
#> L
#>     n     y 
#> 0.934 0.066 
#> 
#> $T
#> T
#>      n      y 
#> 0.9912 0.0088
query_belief(jt1, c("B", "D", "E"), type = "joint")
#> , , B = y
#> 
#>    E
#> D            n           y
#>   y 0.36261346 0.041523361
#>   n 0.09856873 0.007094444
#> 
#> , , B = n
#> 
#>    E
#> D            n           y
#>   y 0.04637955 0.018500278
#>   n 0.41821906 0.007101117

It should be noticed, that the above could also have been achieved by

jt1 <- jt(cp, propagate = "no")
jt1 <- propagate(jt1, prop = "full")

That is; it is possible to postpone the actual propagation.

Example 2: sum-flow with evidence

e2  <- c(A = "y", X = "n")
jt2 <- jt(cp, e2) 
query_belief(jt2, c("B", "D", "E"), type = "joint")
#> , , B = y
#> 
#>    E
#> D           n            y
#>   y 0.3914092 3.615182e-04
#>   n 0.1063963 6.176693e-05
#> 
#> , , B = n
#> 
#>    E
#> D            n            y
#>   y 0.05006263 2.009085e-04
#>   n 0.45143057 7.711638e-05

Notice that, the configuration (D,E,B) = (y,y,n) has changed dramatically as a consequence of the evidence. We can get the probability of the evidence:

query_evidence(jt2)
#> [1] 0.007152638

Example 3: max-flow without evidence

jt3 <- jt(cp, flow = "max")
mpe(jt3)
#>   A   T   E   L   S   B   X   D 
#> "n" "n" "n" "n" "n" "n" "n" "n"

Example 4: max-flow with evidence

e4  <- c(T = "y", X = "y", D = "y")
jt4 <- jt(cp, e4, flow = "max")
mpe(jt4)
#>   A   T   E   L   S   B   X   D 
#> "n" "y" "y" "n" "y" "y" "y" "y"

Notice, that T, E, S, B, X and D has changed from "n" to "y" as a consequence of the new evidence e4.

Example 5: specifying a root node and only collect to save run time

cp5 <- compile(cpt_list(asia, g) , root_node = "X")
jt5 <- jt(cp5, propagate = "collect")

We can only query from the variables in the root clique now but we have ensured that the node of interest, “X”, does indeed live in this clique. The variables are found using get_clique_root.

query_belief(jt5, get_clique_root(jt5), "joint")
#>    E
#> X            n            y
#>   n 0.88559032 0.0004011849
#>   y 0.04019048 0.0738180151

Example 6: Compiling from a list of conditional probabilities

cl  <- cpt_list(asia2)
cp6 <- compile(cl)

Inspection; see if the graph correspond to the cpts

plot(get_graph(cp6))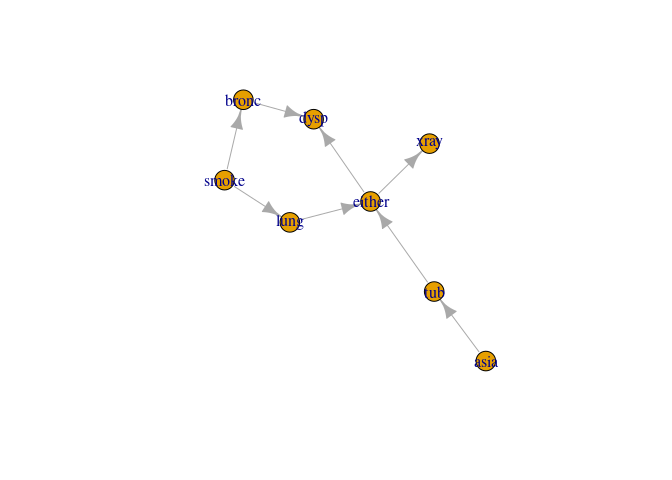

This time we specify that no propagation should be performed

jt6 <- jt(cp6, propagate = "no")

We can now inspect the collecting junction tree and see which cliques are leaves and parents

plot(jt6)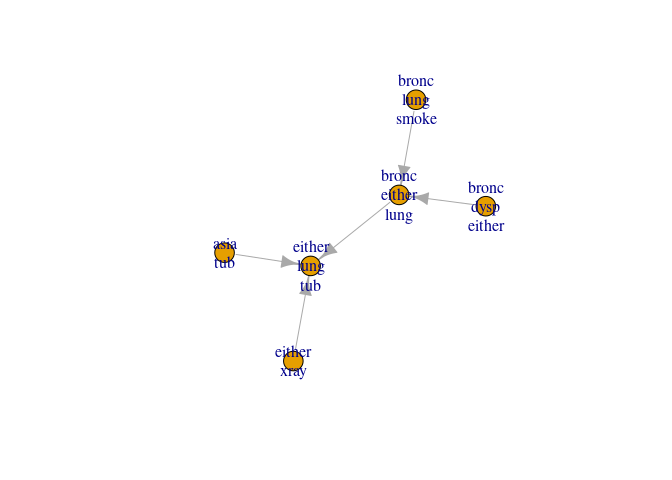

get_cliques(jt6)
#> $C1
#> [1] "asia" "tub" 
#> 
#> $C2
#> [1] "either" "lung"   "tub"   
#> 
#> $C3
#> [1] "bronc"  "either" "lung"  
#> 
#> $C4
#> [1] "bronc" "lung"  "smoke"
#> 
#> $C5
#> [1] "bronc"  "dysp"   "either"
#> 
#> $C6
#> [1] "either" "xray"
get_clique_root(jt6)
#> [1] "either" "lung"   "tub"
jt_leaves(jt6)
#> [1] 1 4 5 6
unlist(jt_parents(jt6))
#> [1] 2 3 3 2

That is; - clique 2 is parent of clique 1 - clique 3 is parent of clique 4 etc.

Next, we send the messages from the leaves to the parents

jt6 <- send_messages(jt6)

Inspect again

plot(jt6)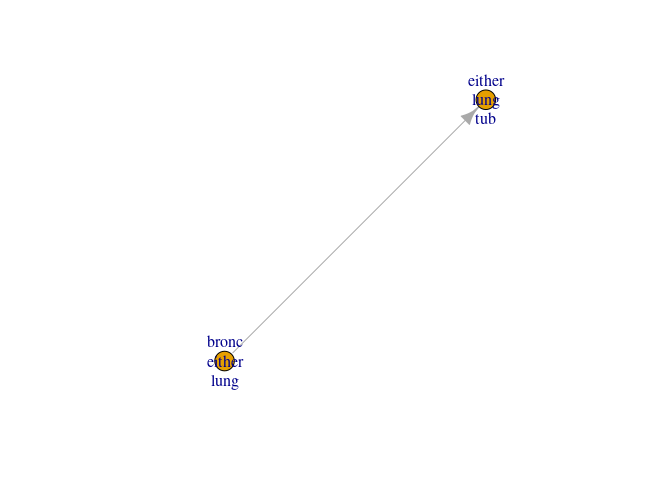

Send the last message to the root and inspect

jt6 <- send_messages(jt6)
plot(jt6)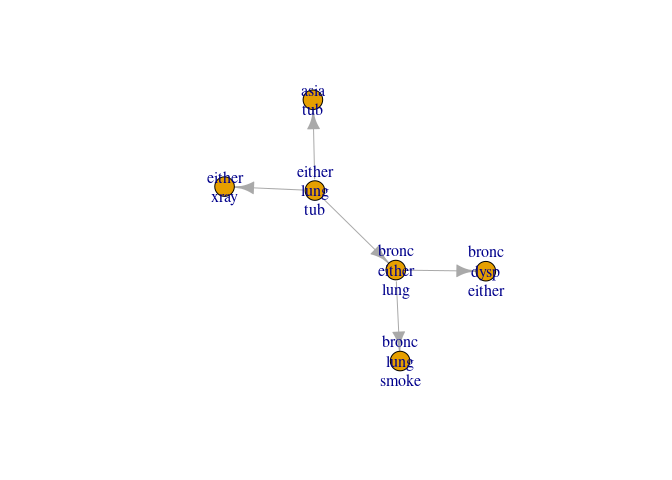

The arrows are now reversed and the outwards (distribute) phase begins

jt_leaves(jt6)
#> [1] 2
jt_parents(jt6)
#> [[1]]
#> [1] 1 3 6

Clique 2 (the root) is now a leave and it has 1, 3 and 6 as parents. Finishing the message passing

jt6 <- send_messages(jt6)
jt6 <- send_messages(jt6)

Queries can now be performed as normal

query_belief(jt6, c("either", "tub"), "joint")
#>       tub
#> either    yes       no
#>    yes 0.0104 0.054428
#>    no  0.0000 0.935172

Example 7: Fitting a decomposable model and apply JTA

We use the ess package (on CRAN), found at https://github.com/mlindsk/ess, to fit an undirected decomposable graph to data.

library(ess)

g7  <- ess::fit_graph(asia, trace = FALSE)
ig7 <- ess::as_igraph(g7)
cp7 <- compile(pot_list(asia, ig7))
jt7 <- jt(cp7)

query_belief(jt7, get_cliques(jt7)[[4]], type = "joint")
#> , , T = n
#> 
#>    L
#> E       n      y
#>   n 0.926 0.0000
#>   y 0.000 0.0652
#> 
#> , , T = y
#> 
#>    L
#> E       n     y
#>   n 0.000 0e+00
#>   y 0.008 8e-04